• Continued from here.
  • Notebook for this post is here.
  • Binary search code itself is here.

max_depth is an interesting parameter.  While n_estimators has a tradeoff between speed & score, max_depth has the possibility of improving both.  By limiting the depth of your trees, you can reduce overfitting.

Unfortunately, deciding on upper & lower bounds is less than straightforward.  It'll depend on your dataset.  Luckily, I found a post on StackOverflow that had a link to a blog post that had a promising methodology.  

First, we build a tree with default arguments and fit it to our data. 

import pandas as pd

from sklearn.metrics import precision_recall_curve
from sklearn.metrics import auc
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import load_breast_cancer


data = load_breast_cancer()
X, y = data.data, data.target

rfArgs = {
    "random_state": 0,
    "n_jobs": -1,
    "class_weight": "balanced",
    "n_estimators": 18,
    "oob_score": True
}

clf = RandomForestClassifier(**rfArgs)
clf.fit(X, y)
Build a tree with default arguments.

Now, let's see how deep the trees get when we don't impose any sort of max_depth. We'll use the code from that wonderful blog post to crawl our Random Forest, and get the height of every tree.

#From here: https://aysent.github.io/2015/11/08/random-forest-leaf-visualization.html
def leaf_depths(tree, node_id = 0):
    '''
    tree.children_left and tree.children_right store ids
    of left and right chidren of a given node
    '''
    left_child = tree.children_left[node_id]
    right_child = tree.children_right[node_id]

    # If a given node is terminal, both left and right children are set to _tree.TREE_LEAF
    if left_child == _tree.TREE_LEAF:
        depths = np.array([0])  # Set depth of terminal nodes to 0
    else:
        # Get depths of left and right children and increment them by 1
        left_depths = leaf_depths(tree, left_child) + 1
        right_depths = leaf_depths(tree, right_child) + 1
 
        depths = np.append(left_depths, right_depths)
 
    return depths

allDepths = [leaf_depths(estimator.tree_) 
             for estimator in clf.estimators_]

print(np.hstack(allDepths).min())
print(np.hstack(allDepths).max())
Get height of every tree.

Here's the output:

#> 2
#> 9
Output of the above

We'll be searching between 2 and 9!  

Let's bring back our old make a helper function to easily return scores.

...

def getForestAccuracy(X, y, kwargs):
    clf = RandomForestClassifier(**kwargs)
    clf.fit(X, y)
    y_pred = clf.oob_decision_function_[:, 1]
    precision, recall, _ = precision_recall_curve(y, y_pred)
    return auc(recall, precision)
Helper function to return score

Now let's see it in action:

max_depth = bgs.compareValsBaseCase(X, 
     y, 
     getForestAccuracy,        
     rfArgs, 
     "max_depth", 
     0, 
     2, 
     9
 )
bgs.showTimeScoreChartAndGraph(max_depth, html=True)
Create chart of max depth.

Here's what we've got:

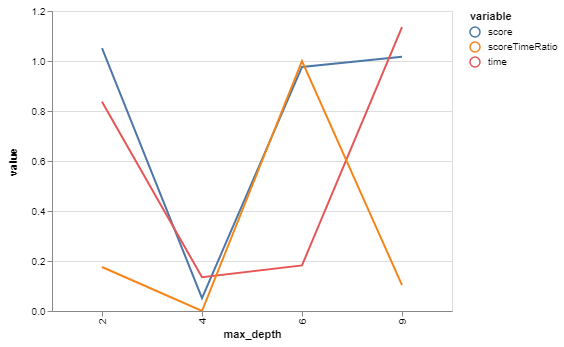
Max depth chart
Max depth chart
max_depth score time
2 0.987707 0.145360
9 0.987029 0.147563
6 0.986247 0.140514
4 0.968316 0.140164

max_depth score time scoreTimeRatio
2 1.051571 0.837377 0.175986
9 1.016649 1.135158 0.103478
6 0.976311 0.182516 1.000000
4 0.051571 0.135158 0.000000

So, for our purposes, 9 will function as our baseline since that was the biggest depth that it built with default arguments.  

Looks like a max_depth of 2 has a slightly higher score than 9, and is slightly faster!  Interestingly, it's slightly slower than  4 or 6.  Not sure why that is.